Exemple: prova T d’igualtat de mitjanes per a dues mostres independents
Es va realitzar una prova estadística per comparar els efectes de dues dietes en malalts d’Alzheimer. Es va comparar el temps que necessitaven per a realitzar un determinat exercici de memòria segons la dieta. La taula següent representa els temps en minuts que van trigar en realitzar l’exercici de memòria, un grup de 7 malalts que seguien la dieta A i un grup de 10 malalts que seguien la dieta B.
| Dieta A | 7.3 | 8.5 | 7.4 | 8.7 | 8.3 | 6.2 | 6.9 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Dieta B | 5.4 | 6.3 | 7.2 | 5.5 | 4.8 | 5.9 | 7.1 | 5.6 | 6.1 | 5.3 |
A realitzar prèviament:
- Especifica el teu directori de treball
- Carrega les dades del fitxer Practica5_exemple.xlsx i guarda-les amb el nom
dades. - Mira les primeres files de la taula de dades que has carregat amb la funció
head() - Fes un resum numèric global de totes les dades:
summary(dades)
## dieta temps ## A: 7 Min. :4.800 ## B:10 1st Qu.:5.600 ## Median :6.300 ## Mean :6.618 ## 3rd Qu.:7.300 ## Max. :8.700
- Fes un resum dels temps en funció de la dieta
Resum numèric per categories:
Resum numèric per cada dieta amb la funció tapply():
tapply(dades$temps, dades$dieta, summary)
## $A ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 6.200 7.100 7.400 7.614 8.400 8.700 ## ## $B ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 4.800 5.425 5.750 5.920 6.250 7.200
Representació gràfica
Diagrama de caixes múltiple amb la funció boxplot()
boxplot(dades$temps~dades$dieta)
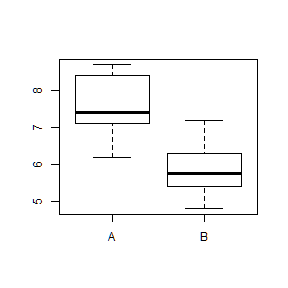
Segons aquests resultats de l’anàlisi descriptiva, els temps per a realitzar l’exercici dels que han seguit la dieta B són en general menors que els de la dieta A. Però per poder confirmar que la dieta B és beneficiosa per als malalts d’Alzheimer haurem de realitzar una prova d’hipòtesis estadística per confirmar que les diferències que estem observant no són només degudes a l’atzar.
Volem saber si les diferències que observem en els temps segons la dieta són significatives o no. Per això plantegem una prova d’hipòtesis per contrastar si els temps mitjans segons les dues dietes són iguals o no:
Test d’igualtat de dues mitjanes per a mostres independents
H_0 : mu_A = mu_B
H_1 : mu_A ≠ mu_B
Tenim dues possibilitats:
- Prova T per a mostres independents, si les dades segueixen una distribució normal.
- Prova de Wilcoxon per a mostres independents, si les dades NO segueixen una distribució normal.
Per tant, el primer que cal fer és una prova de normalitat del temps segons la dieta.
- Test de normalitat Shapiro-Wilk
H_0 : les dades (temps) segueixen una distribució normal
H_1 : les dades (temps) NO segueixen una distribució normal
# Test de normalitat SHAPIRO-WILK del temps per a cada dieta
tapply(dades$temps,dades$dieta,function(x) shapiro.test(x))
## $A ## ## Shapiro-Wilk normality test ## ## data: x ## W = 0.93713, p-value = 0.613 ## ## ## $B ## ## Shapiro-Wilk normality test ## ## data: x ## W = 0.93626, p-value = 0.5122
El p-valor del test de normalitat és en totes dues dietes > 0.05 i per tant no rebutgem \(H_0\). Podem suposar que les dades segueixen una distribució normal. Per tant, per comparar les mitjanes dels temps segons la dieta aplicarem la prova T. Però també en aquest cas hi ha dues possibilitats: que les variàncies dels dos grups siguin iguals o que siguin diferents.
- Prova F d’igualtat de dues variàncies
H_0 : sigma2A = sigma2B
H_1 : sigma2A ≠ sigma2B
Prova F d’igualtat de variàncies amb la funció var.test():
var.test(dades$temps~dades$dieta)
## ## F test to compare two variances ## ## data: dades$temps by dades$dieta ## F = 1.4145, num df = 6, denom df = 9, p-value = 0.614 ## alternative hypothesis: true ratio of variances is not equal to 1 ## 95 percent confidence interval: ## 0.3274609 7.8130789 ## sample estimates: ## ratio of variances ## 1.41454
Com que p-value > 0.05, NO rebutgen H_0; podem assumir que les variàncies en els dos grups són iguals. Ara sabem que hem d’aplicar la prova T d’igualtat de mitjanes amb variàncies iguals:
- Prova T d’igualtat de mitjanes amb variàncies iguals
Utilitzem la funció t.test()amb l’opció var.equal=T
t.test(dades$temps~dades$dieta, var.equal=T)
## ## Two Sample t-test ## ## data: dades$temps by dades$dieta ## t = 4.1123, df = 15, p-value = 0.000923 ## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval: ## 0.8161125 2.5724590 ## sample estimates: ## mean in group A mean in group B ## 7.614286 5.920000
Com que p-value < 0.05, rebutgem H_0; les mitjanes de temps segons la dieta són significativament diferents. Podem afirmar, amb un 95% de confiança que la dieta B és beneficiosa per a la memòria dels malats d’Alzheimer.
Problema 1: Activitat motora ratolins
Es vol comparar l’activitat motora espontània d’un grup de 25 ratolins control y de 25 ratolins drogats amb una certa substància mesurant el número de vegades que passen per davant d’una cèl·lula fotoelèctrica durant 4 hores.
El fitxer de dades Practica5_problema1.xlsx conté les dades relatives al grup al que pertany cada ratolí (0 = control, 1 = drogat), el pes en grams dels ratolins i el número de vegades que passen per davant de la cèl·lula (num).
L’objectiu és determinar si hi ha diferències significatives entre els ratolins drogats i no drogats en
relació a la seva mobilitat. Per fer-ho aplicarem la prova T de comparació de mitjanes, però prèviament
hem de contrastar la igualtat de variàncies. Un altre aspecte que hauríem de contrastar és la normalitat de
les dades.
- Prova de normalitat
1. Contrastar la normalitat de la variable num.
- Prova F d’igualtat de variàncies
Contrasteu si la variància de la variable num entre els dos grups de ratolins (drogats i control) es pot considerar igual o no, és a dir, volem contrastar la igualtat de variàncies. Realitzar el contrast d’hipòtesis:
H_0 : sigma21 = sigma22
H_1 : sigma21 ≠ sigma22
Responeu les següents preguntes:
2. Quin és el p-valor de la prova F d’igualtat de variàncies?
3. Quina hipòtesi acceptarem segons el resultat de la prova F?
- Prova T d’igualtat de mitjanes per mostres independents
Ara l’objectiu és comparar les mitjanes de dues mostres o de dos grups dins una mostra:
H_0 : mu_1 = mu_2
H_1 : mu_1 ≠ mu_2
En el nostre cas, volem contrastar si la variable num (indicador de la capacitat motora) és significativament diferent o no entre els ratolins drogats i els no drogats.
4. Quin és el p-valor de la prova T per la igualtat de les mitjanes?
5. Hi ha diferencies significatives entre el dos tipus de ratolins respecte les mitjanes de la variable num?
Problema 2: Augment de la pressió arterial sistòlica
Es sospita que un determinat producte natural utilitzat per al tractament de certa afecció pot tenir com a efecte secundari un augment de la pressió arterial sistòlica (PAS). Per comprovar-ho es va mesurar la PAS de 60 individus que prenien aquest producte i de 100 individus que no el prenien. Els resultats es troben al fitxer de dades Practica5_problema2.xlsx on es recullen el tractament (0 = no pren el producte, 1 = sí pren el producte) i la PAS de cada individu.
Analitzeu si s’observa un augment de la PAS per als individus que prenen el producte:
6. Quin és el p-valor de la prova F? Quina hipòtesi acceptarem segons el resultat de la prova de F?
7. Quin és el p-valor de la prova T? Quina hipòtesi acceptarem segons el resultat de la prova T?
8. Quina és la conclusió final respecte a l’objectiu inicial de si s’observen diferències en la PAS?