Exemple 1: Relació entre dues variables (Contínua – Categòrica)
La teofilina és utilitzada per al tractament de malaties respiratòries. Amb l’objectiu de determinar l’efecte del sexe en la seva farmacocinètica, es va mesurar l’excreció de teofilina (L/h) en 20 pacients (1 = home, 2 = dona). Influeix el sexe en l’excreció total de teofilina?
(Les dades es troben al fitxer Practica2_teofilina.xlsx)
IMPORTANT : especifica el teu directori de treball (on has guardat el fitxer de dades).
Carrega les dades amb RStudio i guarda-les amb el nom “dades”:
File -> Import Data Set -> From Excel
Mira les primeres files de la taula de dades que has carregat
head(dades)
## Sexe Teofilina ## 1 1 2.25 ## 2 2 5.89 ## 3 1 1.46 ## 4 2 4.05 ## 5 2 4.87 ## 6 2 4.65
Utilitza la funció factor() per especificar que la variable sexe és categòrica (1 = home, 2 = dona). Fes que la nova variable es digui Sexe2 i es guardi dins la taula dades (hauràs d’assignar-li el nom dades$Sexe2):
dades$Sexe2<-factor(dades$Sexe, levels=c(1,2), labels=c("home", "dona"))
Mira de nou les primeres files de la taula de dades per veure si s’ha afegit correctament la nova variable:
head(dades)
## Sexe Teofilina Sexe2 ## 1 1 2.25 home ## 2 2 5.89 dona ## 3 1 1.46 home ## 4 2 4.05 dona ## 5 2 4.87 dona ## 6 2 4.65 dona
A partir d’ara quan volguem analitzar la variable Sexe ho farem amb la nova variable Sexe2.
Anàlisi numèrica d’una variable contínua i una categòrica:
- Resums numèrics de la variable contínua per a cada categoria de la variable categòrica
Utilitzarem la funció tapply() per obtenir els resums numèrics de la variable contínua per a cada categoria de la variable categòriaca:
tapply(dades$Teofilina, dades$Sexe2, summary)
## $home ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 1.460 1.808 2.045 2.028 2.208 2.610 ## ## $dona ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 3.420 4.093 4.565 4.547 4.815 5.890
Representació gràfica d’una variable contínua i una categòrica:
- Diagrama de caixes múltiple
Farem un diagrama de caixes amb la funció boxplot()
Sense cap titol:
boxplot(dades$Teofilina~dades$Sexe2)
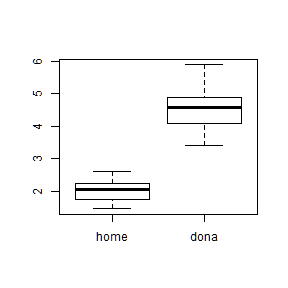
Amb el nom de les dues variables
boxplot(dades$Teofilina~dades$Sexe2,
xlab = "Sexe",
ylab = "Teofilina")

Amb el nom de les dues variables i el títol
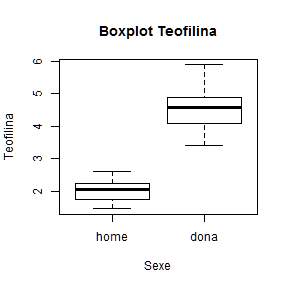
boxplot(dades$Teofilina~dades$Sexe2,
xlab = "Sexe",
ylab="Teofilina",
main = "Boxplot Teofilina")
Exemple 2: Relació entre dues variables (Categòrica – Categòrica)
El fitxer Practica2_cistitis.xlsx conté els resultats de tres tractaments alternatius a la cistitis (Trimethorprim, Amoxicilina, Sulfamethoxazol). Quin dels tres tractaments és més efectiu?
Carrega les dades amb RStudio i guarda-les amb el nom “dades”.
Mira les primeres files de la taula de dades que has carregat
head(dades)
## tractament curat ## 1 T 1 ## 2 T 1 ## 3 T 1 ## 4 T 1 ## 5 T 1 ## 6 T 1
Utilitza la funció factor() per especificar que la variable curat és categòrica (1 = curat, 0 = no curat). Fes que la nova variable es digui curat2 i es guardi dins la taula dades (hauràs d’assignar-li el nom dades$curat2):
dades$curat2<-factor(dades$curat, levels=c(0,1), labels=c("no curat", "curat"))
Mira de nou les primeres files de la taula de dades per veure si s’ha afegit correctament la nova variable:
head(dades)
## tractament curat curat2 ## 1 T 1 curat ## 2 T 1 curat ## 3 T 1 curat ## 4 T 1 curat ## 5 T 1 curat ## 6 T 1 curat
A partir d’ara quan vulguem analitzar la variable curat ho farem amb la nova variable curat2.
Anàlisi numèrica de dues variables categòriques:
- Taula de freqüències 2×2. Taula de contingència
Crea la taula de freqüències absolutes amb la funció table() i anomena-la “taula1”:
taula1 <- table(dades$curat2, dades$tractament)
Visualitza la taula (simplement escriu el nom):
taula1
## ## A S T ## no curat 6 7 2 ## curat 6 3 11
Crea la taula de percentatges total amb la funció prop.table() i anomena-la “taulapt”:
taulapt <- 100*prop.table(table(dades$curat2, dades$tractament))
Crea la taula de percentatges files i anomena-la “taulapf”. Afegeix un 1 al final per indicar que vols fer el percentatge fila:
taulapf <- 100*prop.table(table(dades$curat2, dades$tractament), 1)
Visualitzar el resultat
taulapf
## ## A S T ## no curat 40.00000 46.66667 13.33333 ## curat 30.00000 15.00000 55.00000
Crea la taula de percentatges columnes i anomena-la “taulapc”. Afegeix un 2 al final per indicar que vols fer el percentatge fila:
taulapc <- 100*prop.table(table(dades$curat2, dades$tractament), 2)
Visualitzar el resultat
taulapc
## ## A S T ## no curat 50.00000 70.00000 15.38462 ## curat 50.00000 30.00000 84.61538
Quina de les dues taules és més apropiada (percentatge fila o percentatge columna) per respondre quin dels tres tractaments és més efectiu?
Representació gràfica de dues variables categòriques:
- Diagrama de barres apilat
Amb la funció barplot() farem la representació gràfica de la taula de freqüències absolutes:
barplot(taula1)
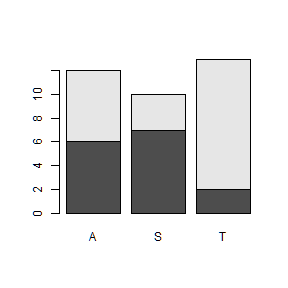
Representació de la taula de percentatges columna
barplot(taulapc)
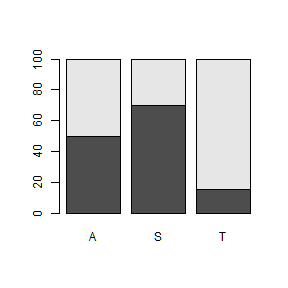
Representació de la taula de percentatges columna en colors blau-grana (2=vermell, 4=blau)
barplot(taulapc, col=c(2,4))

Exemple 3: Relació entre dues variables (Contínua – Contínua)
Les dades següents són els resultats d’un experiment amb E.coli per investigar la seva capacitat de la producció d’Acetyl-CoA sota diferents concentracions de glucosa a la solució nutrient:
| Nombre d’experiment | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Glucosa (mmol/l) | 10 | 20 | 30 | 40 | 50 |
| Producció d’Acetyl-CoA | 2.4 | 3.6 | 5.3 | 7.9 | 8.4 |
Introdueix les dades manualment en dos vectors:
glucosa <- c(10, 20, 30, 40, 50)
acetylcoa <- c(2.4, 3.6, 5.3, 7.9, 8.4)
Representació gràfica de dues variables contínues:
- Diagrama de dispersió i recta de regressió
Amb la funció plot()farem el diagrama de dispersió i amb la funció abline()afegirem la recta de regressió al gràfic:
plot(glucosa, acetylcoa)
abline(lm(acetylcoa~glucosa))

Anàlisi numèrica de dues variables contínues:
- Coeficient de correlació
Amb la funció cor()podem obtenir el coeficient de correlació entre dues variables numèriques:
cor(glucosa,acetylcoa)
## [1] 0.9842163
- Equació de la recta de regressió
La recta de regressió entre X i Y es pot obtenir amb la funció lm()
L’equació de la recta és Y=a+b*X, on a=primer valor numèric (sota de “intercept”) i b=segon valor numèric
lm(acetylcoa~glucosa)
## ## Call: ## lm(formula = acetylcoa ~ glucosa) ## ## Coefficients: ## (Intercept) glucosa ## 0.630 0.163
Pràctica 2: Influència de la dieta sobre els nivells de colesterol
DADES
El fitxer de dades (Practica2_dades.xlsx) conté les següents variables:
id: identificador del pacient.edat: edat en anys del pacient.genere: sexe (1 = H, 2 = D)pes: pes en kg.dieta: identificador de la dieta seguida (1=vegana, 2=mediterrània, 3=fast-food).pas: pressió arterial sistòlica.pad: pressió arterial diastòlica.chdl: colesterol HDL (bó).cldl: colesterol LDL (dolent).
QÜESTIONS
1. Carregueu les dades i guardeu-les en una taula anomenada dades.
2. Mireu les primeres files de la taula de dades que heu carregat.
3. Feu un resum numèric de totes les dades. Creus que el resum de les variables genere i dieta és adequat?
4. Especifiqueu les variables categòriques (genere i dieta) i les etiquetes de les categories: Utilitzeu la funció factor() i guardeu les noves variables amb els noms genere2 i dieta2 dins la taula dades
5. Torneu a fer un resum numèric de totes les dades i mira si el resum numèric de les dues noves variables és adequat.
6. Analitzeu la distribució dels individus en les tres dietes segons el sexe. (Relacionar les variables dieta i genere gràficament i numèricament). Contesteu les següents preguntes:
- Del total de dones, quin percentatge segueix la dieta 1?
- Entre els que segueixen la dieta 1, quin percentatge sòn dones?
- Quin percentatge total d’individus segueix la dieta 1?
7. Analitzeu la relació entre el tipus de dieta i la pressió arterial sistòlica:
- Quin tipus de gràfic és el més adequat?
- Comenta si observes alguna relació.
8. Quina és la pressió arterial sistòlica mitjana dels que segueixen la dieta 1?
9. Hi ha alguna relació entre els nivells de colesterol dolent (CLDL) i el pes dels individus?
- Quin és el coeficient de correlació lineal?
- Quin colesterol mitjà es pot predir a una persona que pesa 70 kg?
10. Es considera que el nivell de colesterol CLDL és normal si és inferior o igual a 100, que és normal-alt si es troba entre 100 i 160, i alt si és superior a 160.
Creeu una nova variable anomenada catcldl que classifiqui els individus en aquest tres nivells:
# Fem una copia de `cldl` en una nova variable `catcldl`
catcldl <- cldl
# Mirem els valors de `catcldl`
catcldl
# Si cldl<=100 li assignem un 1 a la variable `catcldl`
catcldl[cldl<=100] <- 1
# Si cldl>100 li assignem un 2 a la variable `catcldl`
catcldl[cldl>100] <- 2
# Si cldl>160 li assignem un 3 a la variable `catcldl`
catcldl[cldl>160] <- 3
# Mirem els valors
catcldl
11. Definiu aquesta nova variable com a variable categòrica i especifiqueu les etiquetes de les categories. Guardeu-la amb el nom catcldl2:
12. Analitzeu gràficament i numèricament la variable catcldl2.
- Quin percentatge d’individus té un nivell normal-alt de colesterol?
13. Compareu els tres nivells de colesterol CLDL amb el tipus de dieta.
- Del total de persones que segueixen la dieta 3, quin percentatge té nivells alts de colesterol?